Binary tree part 1

2020-05-27

Disclaimer

This article is originally based on my understanding of this concept. No guarantee on the accuracy.😅

Since the root and node share similar structure, it’s natural to use recursion to solve relative problem.

Also, iteration can also be applied. The key would be which kind of data structure to store the data of a tree. Normally, a queue(FIFO) or a stack(FILO) depeding on the traversal order.

Binary Tree in javascript：

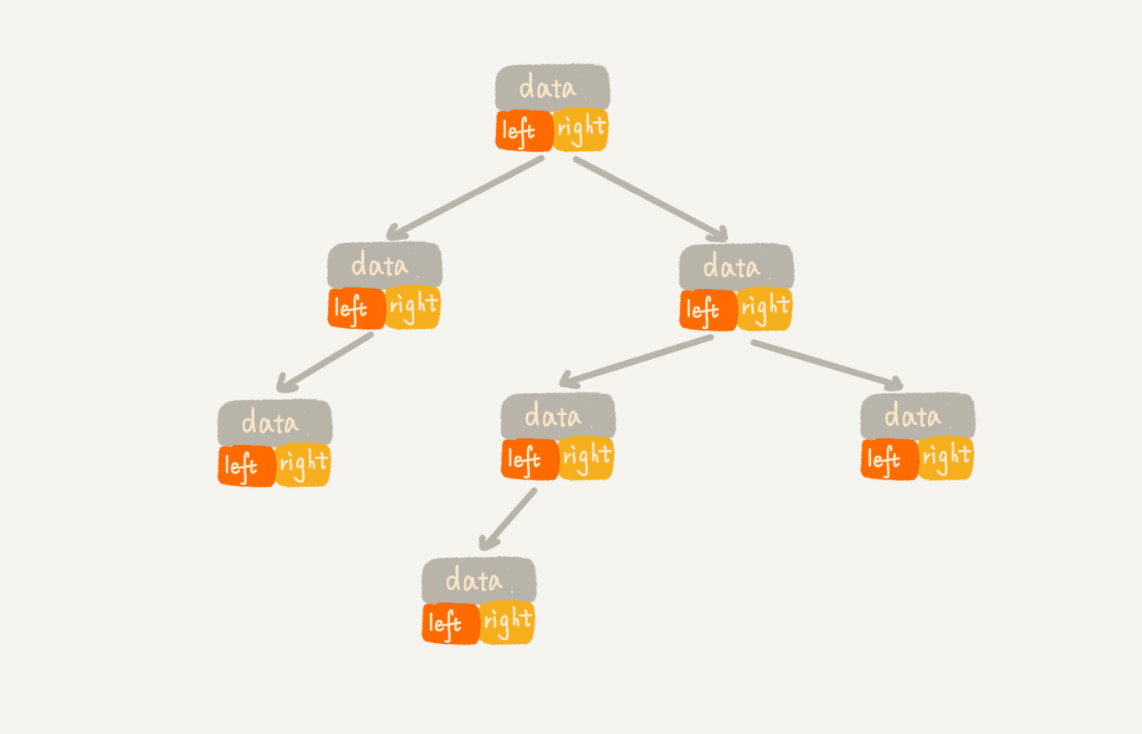
function BinaryTree() {
  let Node = function (val) {
    this.val = val;
    this.left = null;
    this.right = null;
  };
  let root = null;
}

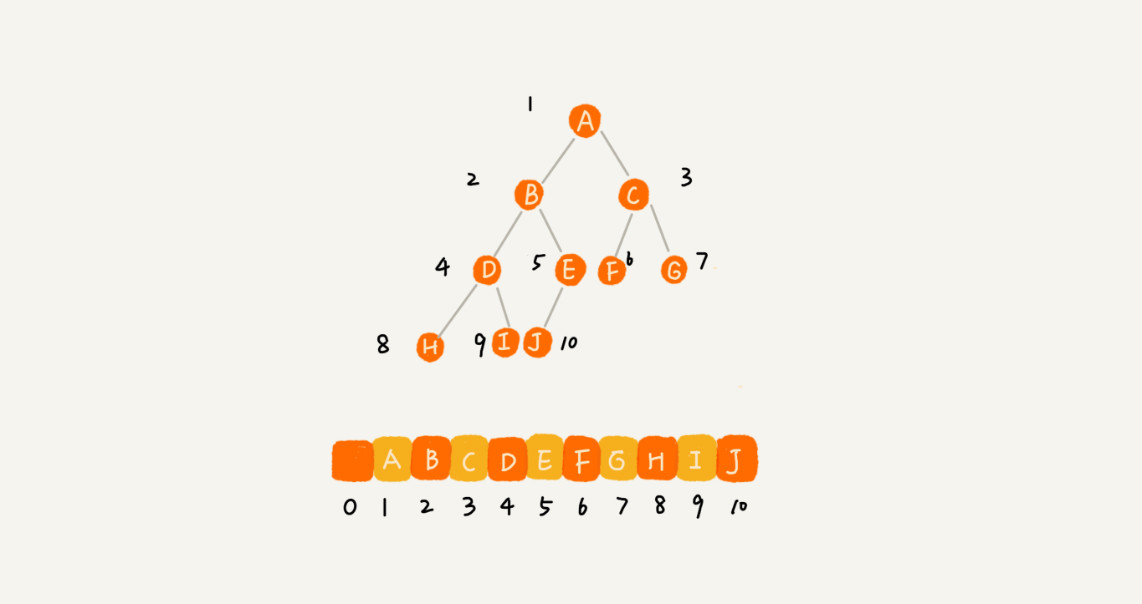
Or using an array to store the elements of the tree where the root node is stored at index 1 not 0.

For complete binary tree, if the index of an element (eg, D, i = 4). Its left child node will be stored in 2*i (H,at 8), and its right childe node will be stored in2 * i-1, its root node will be stored at Math.floor( i/2)

Traversal of tree

Depth-first	Breath-first
Preorder	Level-order
Inorder
Postorder

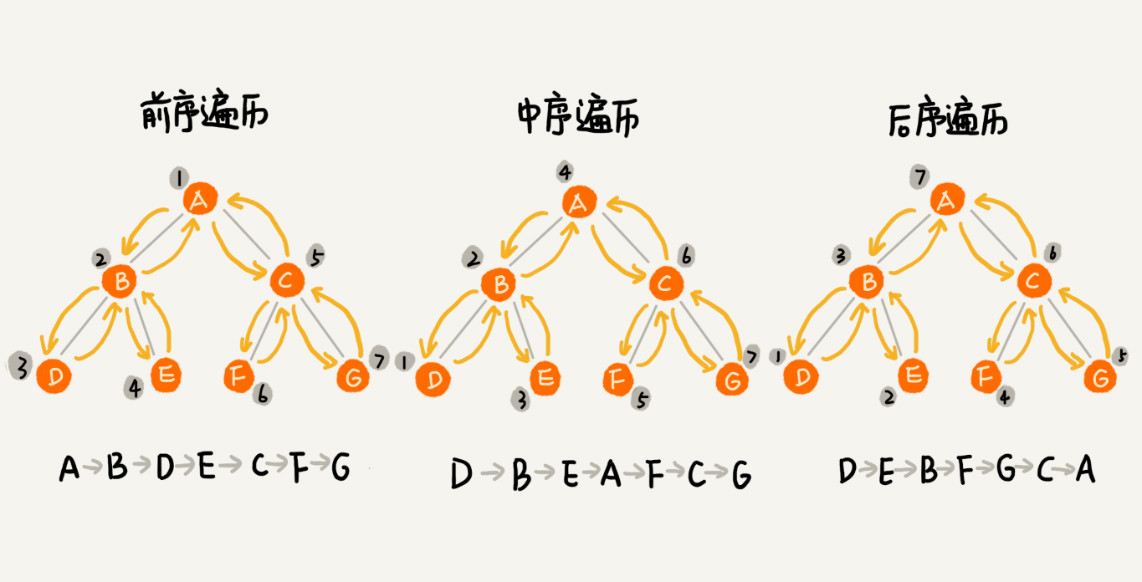
Preorder `(root -> left node ->right node`

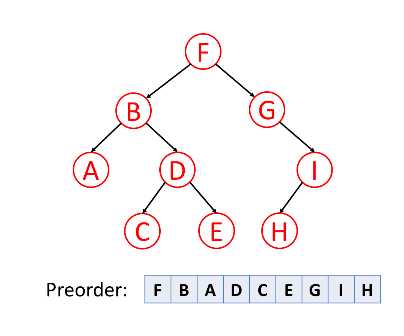
preorder

Recursion:

var preorderTraversal = function (root) {
  const res = [];
  function traversal(root) {
    if (root !== null) {
      //exit point
      //the sequences matters!
      res.push(root.val); // access the root
      traversal(root.left); // left
      traversal(root.right); // right
    }
  }
  traversal(root);
  return res;
};

*Iteration: *

version 1:

const preorderTraversal = (root) => {
  const res = []; //store the values of nodes
  const stack = [root]; //FILO
  if (!root) return res; //exit point
  while (stack.length > 0) {
    let cur = stack.pop(); //pop out the current element
    res.push(cur.val); //push to the result array
    cur.right && stack.push(cur.right); //if has right node, first push it
    cur.left && stack.push(cur.left); //if has left node, then push it
  }
  return res;
};

version 2:

var preorderTraversal = function (root) {
  var result = [];
  var stack = [];
  var p = root;
  while (stack.length != 0 || p != null) {
    if (p != null) {
      stack.push(p);
      result.push(p.val); // Add before going to children
      p = p.left;
    } else {
      var node = stack.pop();
      p = node.right;
    }
  }
  return result;
};

Inorder `left node -> root -> right node`

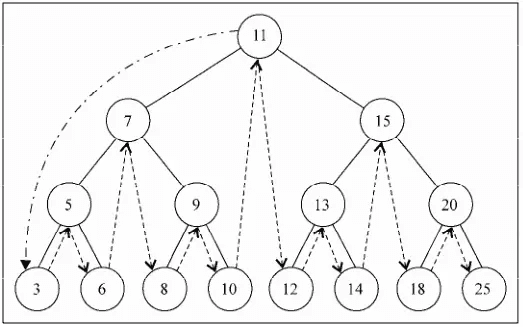
Recursion:

var inorderTraversal = function (root) {
  const res = [];
  function traversal(root) {
    if (root !== null) {
      //exit point
      traversal(root.left); //left node first
      res.push(root.val); //store the root
      traversal(root.right); //right node last
    }
  }
  traversal(root);
  return res;
};

Iteration:

General idea: Using a stack to record the iteration.

If current node has left child node, push it to the stack, and move the current pointer to the left child node.
If the current node dosen’t have left node (either only has right node or dosen’t have any child), obtain the previous node (the root of the current node) by poping the stack and push into the result. Move the current to the right of the previous node.
The exit point is when the satck is empty and current node is pointing to null.

Version 1:

Left && push into the stack 👇 <<————————————————————————————｜
!left && push into result and pop out from the stack mark the left child as visited(null) 👇 ｜
right && push into the stack 👉——————————————————————————————｜

var inorderTraversal = function (root) {
  if (!root) return [];
  let stack = [root],
    res = [],
    cur = root;
  while (stack.length > 0) {
    while (cur.left) {
      stack.push(cur.left);
      cur = cur.left;
    }
    cur = stack.pop();
    res.push(cur.val);
    cur.left = null;
    if (cur.right) {
      stack.push(cur.right);
      cur = cur.right;
    }
  }
  return res;
};

Version 2:

var inorderTraversal = function(root) {
  var result = [];
  var stack = [];
  var p = root;
  while(stack.length!=0 || p != null) {
      if(p != null) {
      stack.push(p);
      p = p.left;
  } else {
      var node = stack.pop();
      result.push(node.val); 
      p = node.right;
  }
  }
  return result;
};

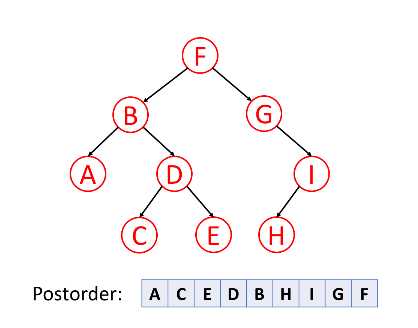
Postorder `left node -> right node->root`

*Recursion: *

var postOrder(root){
	let res=[];
    function traversal(node){
        if(node){
            traversal(node.left)
            traversal(node.rigth)
            res.push(node.val)
        }
    }
    traversal(root);
    return;
}

Iteration: (the reverse of preorder traversal)

Version1:

const postorderTraversal = (root) => {
  if (!root) return [];
  const stack = [root],
    res = [];
  while (stack.length) {
    let curr = stack.pop();
    res.unshift(curr.val); //unshift the current val ->reverse
    curr.left && stack.push(curr.left); //first push left node ->reverse
    curr.rignht && stack.push(curr.right); //then push right node
  }
  return res;
};

Version 2:

var postorderTraversal = function (root) {
  var result = [];
  var stack = [];
  var p = root;
  while (stack.length != 0 || p != null) {
    if (p != null) {
      stack.push(p);
      result.unshift(p.val); // Reverse the process of preorder
      p = p.right; // Reverse the process of preorder
    } else {
      var node = stack.pop();
      p = node.left; // Reverse the process of preorder
    }
  }
  return result;
};

Summary: